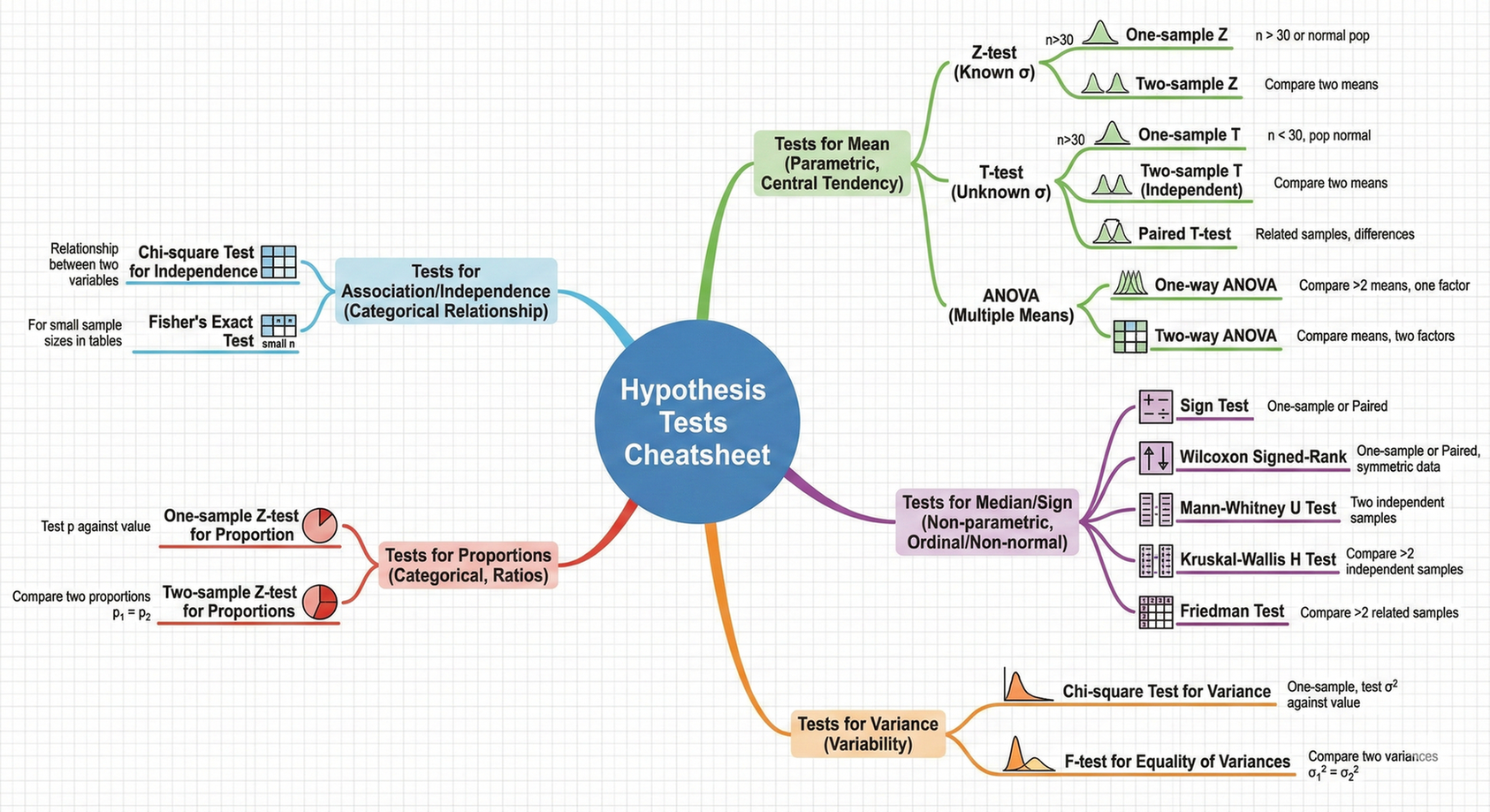
1. Hypothesis Tests in Python

A statistical hypothesis test is a method of statistical inference used to decide whether the data at hand sufficiently support a particular hypothesis. Hypothesis testing allows us to make probabilistic statements about population parameters.

Few Notes:

• When it comes to assumptions such as the expected distribution of data or sample size, the results of a given test are likely to degrade gracefully rather than become immediately unusable if an assumption is violated.
• Generally, data samples need to be representative of the domain and large enough to expose their distribution to analysis.
• In some cases, the data can be corrected to meet the assumptions, such as correcting a nearly normal distribution to be normal by removing outliers, or using a correction to the degrees of freedom in a statistical test when samples have differing variance, to name two examples.

1.1 Normality Tests

This section lists statistical tests that you can use to check if your data has a Gaussian distribution.

Gaussian distribution (also known as normal distribution) is a bell-shaped curve.

1.1.1 Shapiro-Wilk Test

Tests whether a data sample has a Gaussian distribution/Normal distribution.

• Assumptions

  • Observations in each sample are independent and identically distributed (iid).

• Interpretation

  • H0: the sample has a Gaussian distribution.
  • H1: the sample does not have a Gaussian distribution.

• Python Code

  # Example of the Shapiro-Wilk Normality Test
  from scipy.stats import shapiro
  data = [0.873, 2.817, 0.121, -0.945, -0.055, -1.436, 0.360, -1.478, -1.637, -1.869]
  stat, p = shapiro(data)
  print('stat=%.3f, p=%.3f' % (stat, p))
  if p > 0.05:
      print('Probably Gaussian')
  else:
      print('Probably not Gaussian')
  

• Sources

  • scipy.stats.shapiro
  • Shapiro-Wilk test on Wikipedia

1.1.2 D’Agostino’s K^2 Test

Tests whether a data sample has a Gaussian distribution/Normal distribution.

• Assumptions

  • Observations in each sample are independent and identically distributed (iid).

• Interpretation

  • H0: the sample has a Gaussian distribution.
  • H1: the sample does not have a Gaussian distribution.

• Python Code

  # Example of the D'Agostino's K^2 Normality Test
  from scipy.stats import normaltest
  data = [0.873, 2.817, 0.121, -0.945, -0.055, -1.436, 0.360, -1.478, -1.637, -1.869]
  stat, p = normaltest(data)
  print('stat=%.3f, p=%.3f' % (stat, p))
  if p > 0.05:
      print('Probably Gaussian')
  else:
      print('Probably not Gaussian')
  

• Sources

  • scipy.stats.normaltest
  • D'Agostino's K-squared test on Wikipedia

1.1.3 Anderson-Darling Test

Tests whether a data sample has a Gaussian distribution/Normal distribution.

• Assumptions

  • Observations in each sample are independent and identically distributed (iid).

• Interpretation

  • H0: the sample has a Gaussian distribution.
  • H1: the sample does not have a Gaussian distribution.

• Python Code

  # Example of the Anderson-Darling Normality Test
  from scipy.stats import anderson
  data = [0.873, 2.817, 0.121, -0.945, -0.055, -1.436, 0.360, -1.478, -1.637, -1.869]
  result = anderson(data)
  print('stat=%.3f' % (result.statistic))
  for i in range(len(result.critical_values)):
      sl, cv = result.significance_level[i], result.critical_values[i]
      if result.statistic < cv:
          print('Probably Gaussian at the %.1f%% level' % (sl))
      else:
          print('Probably not Gaussian at the %.1f%% level' % (sl))
  

• Sources

  • scipy.stats.anderson
  • Anderson-Darling test on Wikipedia

1.2 Correlation Tests

This section lists statistical tests that you can use to check if two samples are related.

1.2.1 Pearson’s Correlation Coefficient

Tests whether two samples have a linear relationship.

• Assumptions

  • Observations in each sample are independent and identically distributed (iid).
  • Observations in each sample are normally distributed.
  • Observations in each sample have the same variance.

• Interpretation

  • H0: the two samples are independent.
  • H1: there is a dependency between the samples.

• Python Code

  # Example of the Pearson's Correlation test
  from scipy.stats import pearsonr
  data1 = [0.873, 2.817, 0.121, -0.945, -0.055, -1.436, 0.360, -1.478, -1.637, -1.869]
  data2 = [0.353, 3.517, 0.125, -7.545, -0.555, -1.536, 3.350, -1.578, -3.537, -1.579]
  stat, p = pearsonr(data1, data2)
  print('stat=%.3f, p=%.3f' % (stat, p))
  if p > 0.05:
      print('Probably independent')
  else:
      print('Probably dependent')
  

• Sources

  • scipy.stats.pearsonr
  • Pearson's correlation coefficient on Wikipedia

1.2.2 Spearman’s Rank Correlation

Tests whether two samples have a monotonic relationship.

• Assumptions

  • Observations in each sample are independent and identically distributed (iid).
  • Observations in each sample can be ranked.

• Interpretation

  • H0: the two samples are independent.
  • H1: there is a dependency between the samples.

• Python Code

  # Example of the Spearman's Rank Correlation Test
  from scipy.stats import spearmanr
  data1 = [0.873, 2.817, 0.121, -0.945, -0.055, -1.436, 0.360, -1.478, -1.637, -1.869]
  data2 = [0.353, 3.517, 0.125, -7.545, -0.555, -1.536, 3.350, -1.578, -3.537, -1.579]
  stat, p = spearmanr(data1, data2)
  print('stat=%.3f, p=%.3f' % (stat, p))
  if p > 0.05:
      print('Probably independent')
  else:
      print('Probably dependent')
  

• Sources

  • scipy.stats.spearmanr
  • Spearman's rank correlation coefficient on Wikipedia

1.2.3 Kendall’s Rank Correlation

Tests whether two samples have a monotonic relationship.

• Assumptions

  • Observations in each sample are independent and identically distributed (iid).
  • Observations in each sample can be ranked.

• Interpretation

  • H0: the two samples are independent.
  • H1: there is a dependency between the samples.

• Python Code

  # Example of the Kendall's Rank Correlation Test
  from scipy.stats import kendalltau
  data1 = [0.873, 2.817, 0.121, -0.945, -0.055, -1.436, 0.360, -1.478, -1.637, -1.869]
  data2 = [0.353, 3.517, 0.125, -7.545, -0.555, -1.536, 3.350, -1.578, -3.537, -1.579]
  stat, p = kendalltau(data1, data2)
  print('stat=%.3f, p=%.3f' % (stat, p))
  if p > 0.05:
      print('Probably independent')
  else:
      print('Probably dependent')
  

• Sources

  • scipy.stats.kendalltau
  • Kendall rank correlation coefficient on Wikipedia

1.2.4 Chi-Squared Test

Tests whether two categorical variables are related or independent.

• Assumptions

  • Observations used in the calculation of the contingency table are independent.
  • 25 or more examples in each cell of the contingency table.

• Interpretation

  • H0: the two samples are independent.
  • H1: there is a dependency between the samples.

• Python Code

  # Example of the Chi-Squared Test
  from scipy.stats import chi2_contingency
  table = [[10, 20, 30],[6,  9,  17]]
  stat, p, dof, expected = chi2_contingency(table)
  print('stat=%.3f, p=%.3f' % (stat, p))
  if p > 0.05:
      print('Probably independent')
  else:
      print('Probably dependent')
  

• Sources

  • scipy.stats.chi2_contingency
  • Chi-Squared test on Wikipedia

1.3 Stationary Tests

This section lists statistical tests that you can use to check if a time series is stationary or not.

1.3.1 Augmented Dickey-Fuller Unit Root Test

Tests whether a time series has a unit root, e.g. has a trend or more generally is autoregressive.

• Assumptions

  • Observations in are temporally ordered.

• Interpretation

  • H0: a unit root is present (series is non-stationary).
  • H1: a unit root is not present (series is stationary).

• Python Code

  # Example of the Augmented Dickey-Fuller unit root test
  from statsmodels.tsa.stattools import adfuller
  data = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
  stat, p, lags, obs, crit, t = adfuller(data)
  print('stat=%.3f, p=%.3f' % (stat, p))
  if p > 0.05:
      print('Probably not Stationary')
  else:
      print('Probably Stationary')
  

• Sources

  • statsmodels.tsa.stattools.adfuller API.
  • Augmented Dickey--Fuller test, Wikipedia.

1.3.2 Kwiatkowski-Phillips-Schmidt-Shin

Tests whether a time series is trend stationary or not.

• Assumptions

  • Observations in are temporally ordered.

• Interpretation

  • H0: the time series is trend-stationary.
  • H1: the time series is not trend-stationary.

• Python Code

  # Example of the Kwiatkowski-Phillips-Schmidt-Shin test
  from statsmodels.tsa.stattools import kpss
  data = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
  stat, p, lags, crit = kpss(data)
  print('stat=%.3f, p=%.3f' % (stat, p))
  if p > 0.05:
      print('Probably Stationary')
  else:
      print('Probably not Stationary')
  

• Sources

  • statsmodels.tsa.stattools.kpss API.
  • KPSS test, Wikipedia.

1.4 Parametric Statistical Hypothesis Tests

This section lists statistical tests that you can use to compare data samples.

1.4.1 Student’s t-test

Tests whether the means of two independent samples are significantly different.

• Assumptions

  • Observations in each sample are independent and identically distributed (iid).
  • Observations in each sample are normally distributed.
  • Observations in each sample have the same variance.

• Interpretation

  • H0: the means of the samples are equal.
  • H1: the means of the samples are unequal.

• Python Code

  # Example of the Student's t-test
  from scipy.stats import ttest_ind
  data1 = [0.873, 2.817, 0.121, -0.945, -0.055, -1.436, 0.360, -1.478, -1.637, -1.869]
  data2 = [1.142, -0.432, -0.938, -0.729, -0.846, -0.157, 0.500, 1.183, -1.075, -0.169]
  stat, p = ttest_ind(data1, data2)
  print('stat=%.3f, p=%.3f' % (stat, p))
  if p > 0.05:
      print('Probably the same distribution')
  else:
      print('Probably different distributions')
  

• Sources

  • scipy.stats.ttest_ind
  • Student's t-test on Wikipedia

1.4.2 Paired Student’s t-test

Tests whether the means of two independent samples are significantly different.

• Assumptions

  • Observations in each sample are independent and identically distributed (iid).
  • Observations in each sample are normally distributed.
  • Observations in each sample have the same variance.
  • Observations across each sample are paired.

• Interpretation

  • H0: the means of the samples are equal.
  • H1: the means of the samples are unequal.

• Python Code

  # Example of the Paired Student's t-test
  from scipy.stats import ttest_rel
  data1 = [0.873, 2.817, 0.121, -0.945, -0.055, -1.436, 0.360, -1.478, -1.637, -1.869]
  data2 = [1.142, -0.432, -0.938, -0.729, -0.846, -0.157, 0.500, 1.183, -1.075, -0.169]
  stat, p = ttest_rel(data1, data2)
  print('stat=%.3f, p=%.3f' % (stat, p))
  if p > 0.05:
      print('Probably the same distribution')
  else:
      print('Probably different distributions')
  

• Sources

  • scipy.stats.ttest_rel
  • Student's t-test on Wikipedia

1.4.3 Analysis of Variance Test (ANOVA)

Tests whether the means of two or more independent samples are significantly different.

• Assumptions

  • Observations in each sample are independent and identically distributed (iid).
  • Observations in each sample are normally distributed.
  • Observations in each sample have the same variance.

• Interpretation

  • H0: the means of the samples are equal.
  • H1: the means of the samples are unequal.

• Python Code

  # Example of the Analysis of Variance Test
  from scipy.stats import f_oneway
  data1 = [0.873, 2.817, 0.121, -0.945, -0.055, -1.436, 0.360, -1.478, -1.637, -1.869]
  data2 = [1.142, -0.432, -0.938, -0.729, -0.846, -0.157, 0.500, 1.183, -1.075, -0.169]
  data3 = [-0.208, 0.696, 0.928, -1.148, -0.213, 0.229, 0.137, 0.269, -0.870, -1.204]
  stat, p = f_oneway(data1, data2, data3)
  print('stat=%.3f, p=%.3f' % (stat, p))
  if p > 0.05:
      print('Probably the same distribution')
  else:
      print('Probably different distributions')
  

• Sources

  • scipy.stats.f_oneway
  • Analysis of variance on Wikipedia

1.4.4 Repeated Measures ANOVA Test

Tests whether the means of two or more paired samples are significantly different.

• Assumptions

  • Observations in each sample are independent and identically distributed (iid).
  • Observations in each sample are normally distributed.
  • Observations in each sample have the same variance.
  • Observations across each sample are paired.

• Interpretation

  • H0: the means of the samples are equal.
  • H1: one or more of the means of the samples are unequal.

• Python Code

  # Currently not supported in Python. :(
  

• Sources

  • Analysis of variance on Wikipedia

1.5 Nonparametric Statistical Hypothesis Tests

In Non-Parametric tests, we don't make any assumption about the parameters for the given population or the population we are studying. In fact, these tests don't depend on the population. Hence, there is no fixed set of parameters is available, and also there is no distribution (normal distribution, etc.)

1.5.1 Mann-Whitney U Test

Tests whether the distributions of two independent samples are equal or not.

• Assumptions

  • Observations in each sample are independent and identically distributed (iid).
  • Observations in each sample can be ranked.

• Interpretation

  • H0: the distributions of both samples are equal.
  • H1: the distributions of both samples are not equal.

• Python Code

  # Example of the Mann-Whitney U Test
  from scipy.stats import mannwhitneyu
  data1 = [0.873, 2.817, 0.121, -0.945, -0.055, -1.436, 0.360, -1.478, -1.637, -1.869]
  data2 = [1.142, -0.432, -0.938, -0.729, -0.846, -0.157, 0.500, 1.183, -1.075, -0.169]
  stat, p = mannwhitneyu(data1, data2)
  print('stat=%.3f, p=%.3f' % (stat, p))
  if p > 0.05:
      print('Probably the same distribution')
  else:
      print('Probably different distributions')
  

• Sources

  • scipy.stats.mannwhitneyu
  • Mann-Whitney U test on Wikipedia

1.5.2 Wilcoxon Signed-Rank Test

Tests whether the distributions of two paired samples are equal or not.

• Assumptions

  • Observations in each sample are independent and identically distributed (iid).
  • Observations in each sample can be ranked.
  • Observations across each sample are paired.

• Interpretation

  • H0: the distributions of both samples are equal.
  • H1: the distributions of both samples are not equal.

• Python Code

  # Example of the Wilcoxon Signed-Rank Test
  from scipy.stats import wilcoxon
  data1 = [0.873, 2.817, 0.121, -0.945, -0.055, -1.436, 0.360, -1.478, -1.637, -1.869]
  data2 = [1.142, -0.432, -0.938, -0.729, -0.846, -0.157, 0.500, 1.183, -1.075, -0.169]
  stat, p = wilcoxon(data1, data2)
  print('stat=%.3f, p=%.3f' % (stat, p))
  if p > 0.05:
      print('Probably the same distribution')
  else:
      print('Probably different distributions')
  

• Sources

  • scipy.stats.wilcoxon
  • Wilcoxon signed-rank test on Wikipedia

1.5.3 Kruskal-Wallis H Test

Tests whether the distributions of two or more independent samples are equal or not.

• Assumptions

  • Observations in each sample are independent and identically distributed (iid).
  • Observations in each sample can be ranked.

• Interpretation

  • H0: the distributions of all samples are equal.
  • H1: the distributions of one or more samples are not equal.

• Python Code

  # Example of the Kruskal-Wallis H Test
  from scipy.stats import kruskal
  data1 = [0.873, 2.817, 0.121, -0.945, -0.055, -1.436, 0.360, -1.478, -1.637, -1.869]
  data2 = [1.142, -0.432, -0.938, -0.729, -0.846, -0.157, 0.500, 1.183, -1.075, -0.169]
  stat, p = kruskal(data1, data2)
  print('stat=%.3f, p=%.3f' % (stat, p))
  if p > 0.05:
      print('Probably the same distribution')
  else:
      print('Probably different distributions')
  

• Sources

  • scipy.stats.kruskal
  • Kruskal-Wallis one-way analysis of variance on Wikipedia

1.5.4 Friedman Test

Tests whether the distributions of two or more paired samples are equal or not.

• Assumptions

  • Observations in each sample are independent and identically distributed (iid).
  • Observations in each sample can be ranked.
  • Observations across each sample are paired.

• Interpretation

  • H0: the distributions of all samples are equal.
  • H1: the distributions of one or more samples are not equal.

• Python Code

  # Example of the Friedman Test
  from scipy.stats import friedmanchisquare
  data1 = [0.873, 2.817, 0.121, -0.945, -0.055, -1.436, 0.360, -1.478, -1.637, -1.869]
  data2 = [1.142, -0.432, -0.938, -0.729, -0.846, -0.157, 0.500, 1.183, -1.075, -0.169]
  data3 = [-0.208, 0.696, 0.928, -1.148, -0.213, 0.229, 0.137, 0.269, -0.870, -1.204]
  stat, p = friedmanchisquare(data1, data2, data3)
  print('stat=%.3f, p=%.3f' % (stat, p))
  if p > 0.05:
      print('Probably the same distribution')
  else:
      print('Probably different distributions')
  

• Sources

  • scipy.stats.friedmanchisquare
  • Friedman test on Wikipedia

1.6 Equality of variance test

Test is used to assess the equality of variance between two different samples.

1.6.1 Levene's test

Levene’s test is used to assess the equality of variance between two or more different samples.

• Assumptions

  • The samples from the populations under consideration are independent.
  • The populations under consideration are approximately normally distributed.

• Interpretation

  • H0: All the samples variances are equal
  • H1: At least one variance is different from the rest

• Python Code

  # Example of the Levene's test
  from scipy.stats import levene
  a = [8.88, 9.12, 9.04, 8.98, 9.00, 9.08, 9.01, 8.85, 9.06, 8.99]
  b = [8.88, 8.95, 9.29, 9.44, 9.15, 9.58, 8.36, 9.18, 8.67, 9.05]
  c = [8.95, 9.12, 8.95, 8.85, 9.03, 8.84, 9.07, 8.98, 8.86, 8.98]
  stat, p = levene(a, b, c)
  print('stat=%.3f, p=%.3f' % (stat, p))
  if p > 0.05:
      print('Probably the same variances')
  else:
      print('Probably at least one variance is different from the rest')
  

• Sources

  • scipy.stats.levene
  • Levene's test on Wikipedia

Source: https://machinelearningmastery.com/statistical-hypothesis-tests-in-python-cheat-sheet/